Parallelized Mandelbrot Generator using OpenMP

Introduction
A Mandelbrot set is defined as the set of all complex numbers ${c}$ for which the generator function:
$f_c(z) = z^2 + c$
remains bounded (i.e., does not diverge to $\pm \infty$). We start with $z=0$ and iteratively evaluate $f_c$ as follows:
$[f_c(0), f_c(f_c(0)), f_c(f_c(f_c(0))),\dots]$
Defining Divergence
| Traditionally, divergence is defined by a threshold of the magnitude of the current element in the sequence. For example, if we choose a threshold of $f_{max} = 10$, then the sequence diverges at the $i^{th}$ iteration if $ | f_c(i) | > f_{max} = 10$. |
Methods
Approach A: Fine-Grained Parallelization
- Pixel-level parallelization, each thread evolves the Mandelbrot set for differnt starting values $c$ in the complex plane.
- Poor scaling due to critical access of shared data buffer.
Approach B: Parallel Frame Generation for Zoom Animation
- Frame-by-frame parallelization when generating multiple frames of the Mandelbrot set at different scales to create a movie (i.e. zooming into one point of the plane).
- Each frame is assigned to a different thread for parallel processing.
- The generated frames are then compiled into a video.
- Much more efficient scaling, each thread works on independent chunck of data
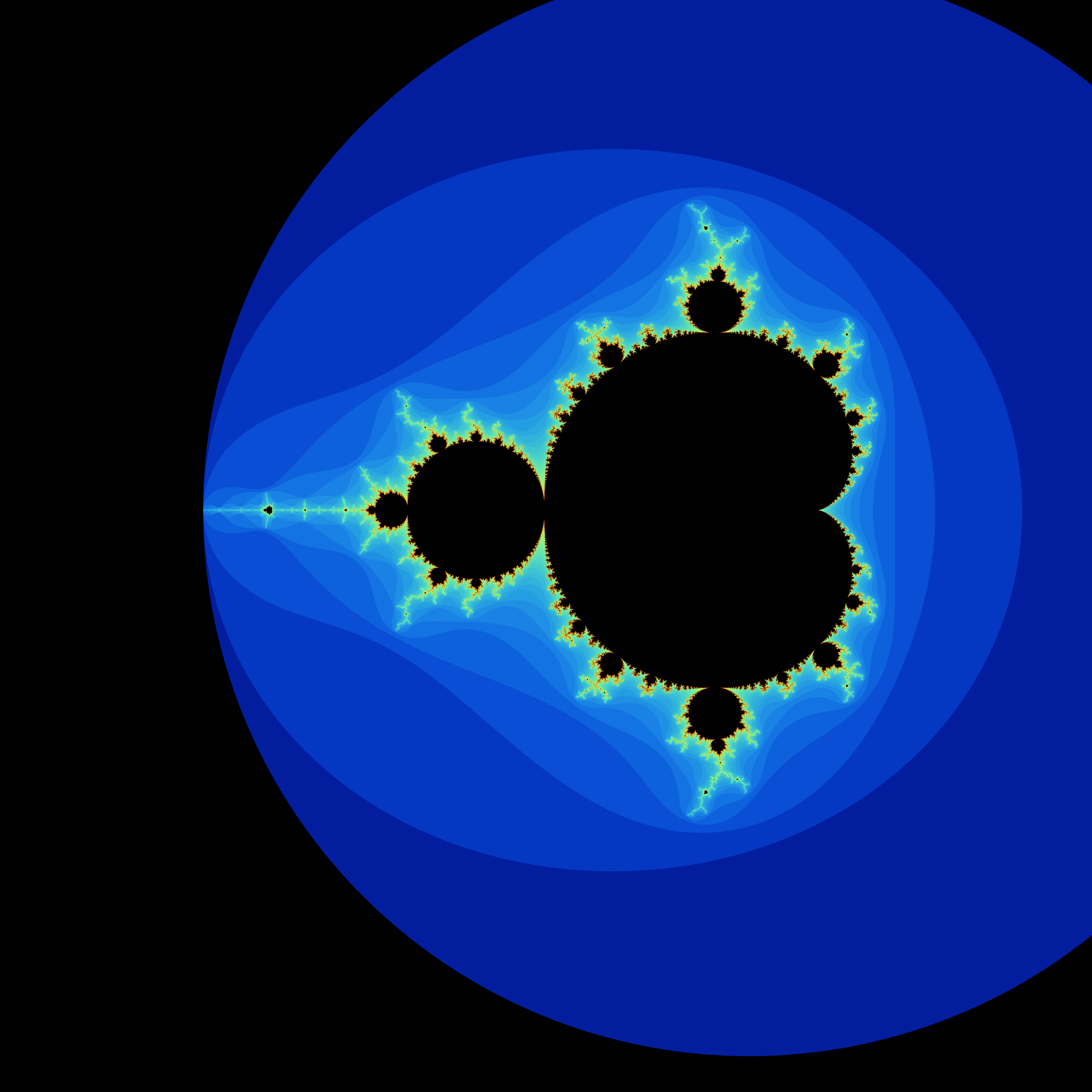
Generated Outputs
Mandelbrot Image

Mandelbrot Zoom Animation
Generated animation of the Mandelbrot set zooming into specific regions:
-
Seahorse Valley $(-0.743643887037151 + 0.131825904205330i)$: Download Seahorse.mp4

-
Elephant Valley $(0.282 + 0.5307i)$: Download Elephant.mp4

-
Feigenbaum Point $(-1.401155 + 0i)$: Download Feigenbaum.mp4
The colormap uses the Escape-Time Algorithm to provide a cool visualization of the complex plane.
Running the Project
See my project Github for source code.
Future Improvements
- Implement GPU acceleration using CUDA.
- Optimize frame generation with better load balancing.
- Enable dynamic thresholding to improve visualization quality.
- Reuse computation between frames.

